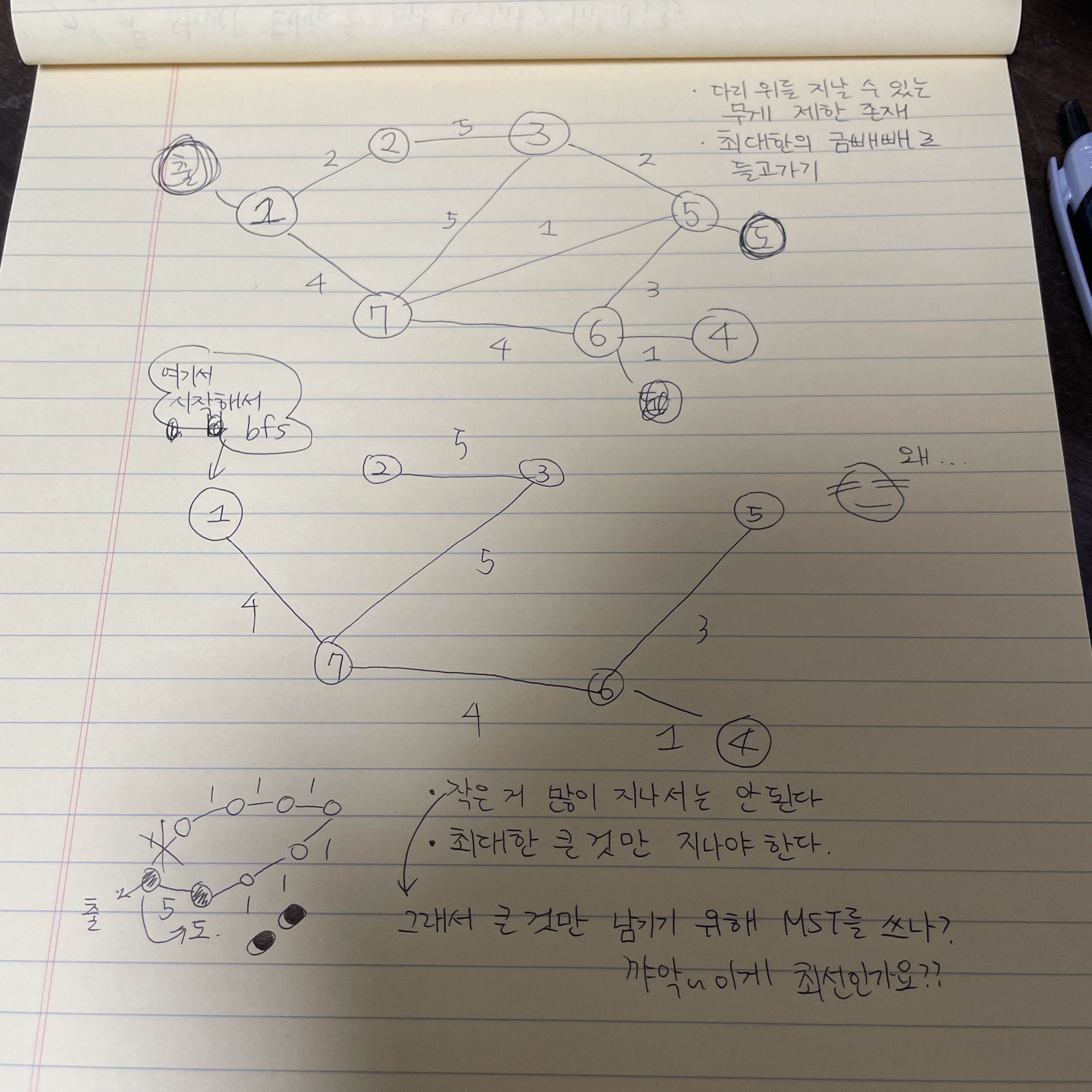
와 mst 분류 몰랐다면 못 풀었을 것 같다. 이번 기회에 mst만 쭉쭉 풀면서 감 잡아봐야겠다.
일단 작은 수는 안 지나는게 이득이라 먼저 큰 수만 남긴다. (역 mst?)
그러곤 출발지에서 도착지로 bfs로 구하면 되겠다 싶었다.
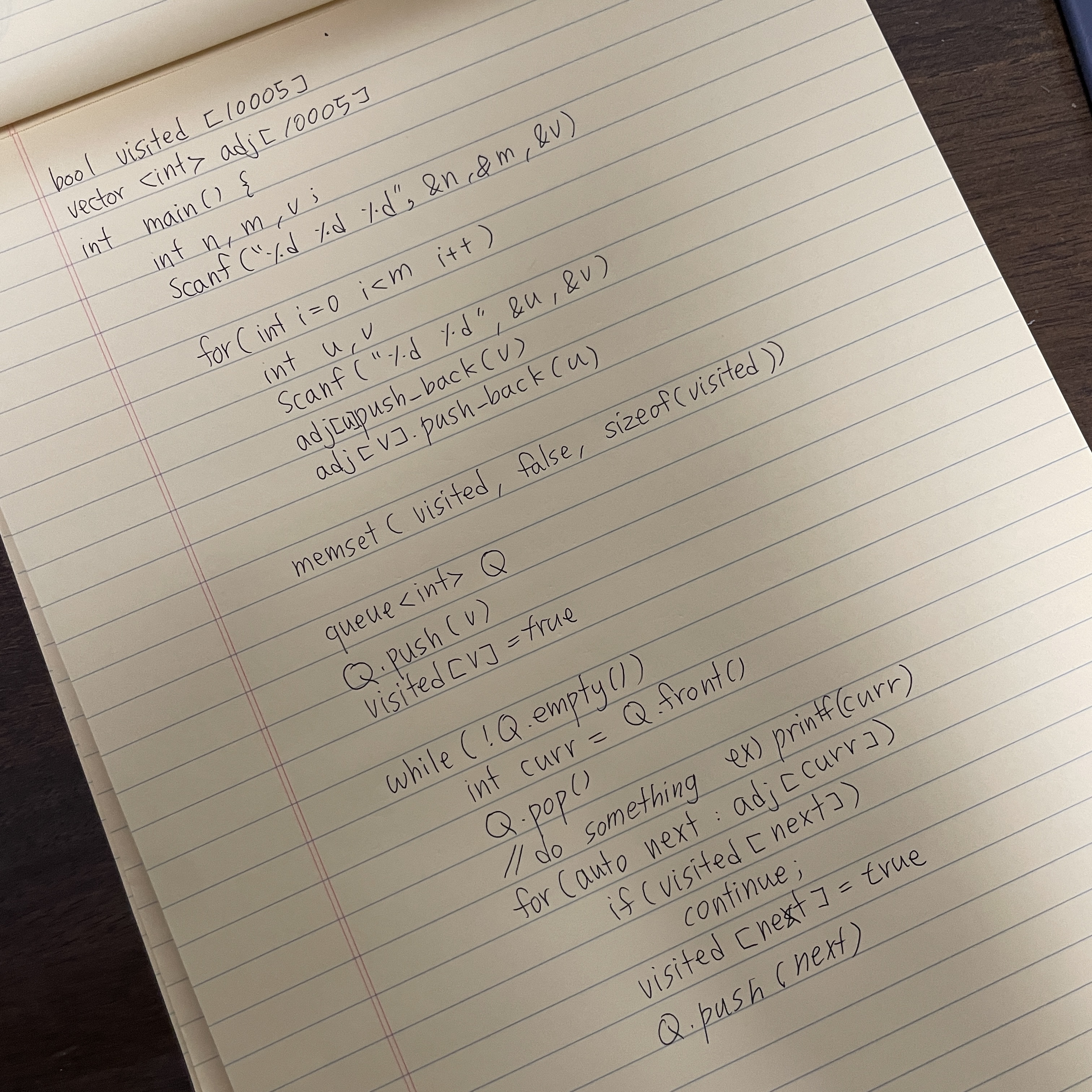
여담이지만 마찬가지로 bfs도 손으로 적으면서 다시 익혔다. 두어번 적으면 외워지더라.
그래서 mst도 bfs도 이제 블로그 코드 안 보고 짤 수 있다! 그런 든든한 마음으로 문제를 풀기 시작했다.
막힌 부분이 두 부분 있었는데,
1. bfs에서 간선을 계산할 때 가중치 정보도 필요했다.
-> 최선인지 모르겠지만 다음 노드와 가중치를 함께 저장했다
for (auto e: edge){
if (Find(e.u) == Find(e.v))
continue;
Merge(e.u, e.v);
adj[e.u].emplace_back(e.v, e.d);
adj[e.v].emplace_back(e.u, e.d);
}2. 단순히 최솟값을 구하면 안 되고 해당 경로의 최솟값을 구해야 한다.
-> 처음에 bfs 순회하면서 최솟값을 갱신했는데 그럼 그냥 모든 간선의 최솟값을 구하게 된다......
-> 이건 고민하다 몰라서 찾아봤는데 dp처럼 경로의 최솟값을 저장하면 된다(!!!)
그리고 한 다섯 번 또 틀렸다.
이유: 갈 수 없는 경우가 있었다......
생각해보면 문제에서 모든 간선들이 연결되어 있다는 정보가 없긴 했다. (이런 정보는 알려주면 안 되나요??????)
나의 코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <functional>
#include <string>
#include <queue>
#include <deque>
#include <stack>
#include <set>
#include <map>
#include <cmath>
#include <cstring>
#include <bitset>
#include <stdio.h>
#include <math.h>
#include <sstream>
#define xx first
#define yy second
#define all(x) (x).begin(), (x).end()
using namespace std;
using i64 = long long int;
using ii = pair<int, int>;
using iis = pair<int, string>;
using ii64 = pair<i64, i64>;
using iii = tuple<int, int, int>;
bool visited[100005];
vector<ii> adj[100005];
struct Edge {
int u, v, d;
};
int par[100005];
int Find(int x) {
if (x == par[x])
return x;
return par[x] = Find(par[x]);
}
void Merge(int x, int y) {
x = Find(x);
y = Find(y);
par[x] = y;
}
void Init(int n) {
for (int i = 1; i <= n; i++) {
par[i] = i;
}
}
int main()
{
int n, m;
int start, end;
scanf("%d %d %d %d", &n, &m, &start, &end);
Init(n);
vector<Edge> edge(m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &edge[i].u, &edge[i].v, &edge[i].d);
}
sort(all(edge), [](const Edge &l, const Edge &r) {
return l.d > r.d;
});
for (auto e: edge){
if (Find(e.u) == Find(e.v))
continue;
Merge(e.u, e.v);
adj[e.u].emplace_back(e.v, e.d);
adj[e.v].emplace_back(e.u, e.d);
}
memset(visited, false, sizeof(visited));
vector<int> cost(n + 5, 987654321);
queue<ii> Q;
Q.push(make_pair(start, 987654321));
visited[start] = true;
while(!Q.empty()) {
ii curr = Q.front();
Q.pop();
// printf("%d %d\n", curr.xx, curr.yy);
for (auto next: adj[curr.xx]) {
if (visited[next.xx])
continue;
visited[next.xx] = true;
cost[next.xx] = min(cost[curr.xx], next.yy);
Q.push(next);
}
}
if (cost[end] == 987654321)
printf("0\n");
else printf("%d\n", cost[end]);
return 0;
}
+ 북님 조언
헐!!! 생각해보니 BFS를 돌릴 필요가 없다.
mst를 수행하다가 find(s) == find(e)인 경우 두 정점간의 경로가 생기기 때문에 이 때 간선의 길이를 출력하면 된다!!!!!
최댓값부터 확인해서 find(s) == find(e)가 되는 순간이 가장 작은 길이가 됨!!!!!!!!!!!!
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <functional>
#include <string>
#include <queue>
#include <deque>
#include <stack>
#include <set>
#include <map>
#include <cmath>
#include <cstring>
#include <bitset>
#include <stdio.h>
#include <math.h>
#include <sstream>
#define xx first
#define yy second
#define all(x) (x).begin(), (x).end()
using namespace std;
using i64 = long long int;
using ii = pair<int, int>;
using iis = pair<int, string>;
using ii64 = pair<i64, i64>;
using iii = tuple<int, int, int>;
bool visited[100005];
vector<ii> adj[100005];
struct Edge {
int u, v, d;
};
int par[100005];
int Find(int x) {
if (x == par[x])
return x;
return par[x] = Find(par[x]);
}
void Merge(int x, int y) {
x = Find(x);
y = Find(y);
par[x] = y;
}
void Init(int n) {
for (int i = 1; i <= n; i++) {
par[i] = i;
}
}
int main()
{
int n, m;
int start, end;
scanf("%d %d %d %d", &n, &m, &start, &end);
Init(n);
vector<Edge> edge(m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &edge[i].u, &edge[i].v, &edge[i].d);
}
sort(all(edge), [](const Edge &l, const Edge &r) {
return l.d > r.d;
});
for (auto e: edge){
if (Find(e.u) == Find(e.v))
continue;
Merge(e.u, e.v);
adj[e.u].emplace_back(e.v, e.d);
adj[e.v].emplace_back(e.u, e.d);
if (Find(start) == Find(end)) {
printf("%d\n", e.d);
return 0;
}
}
printf("0\n");
return 0;
}
'백준' 카테고리의 다른 글
| 22116 창영이와 퇴근 (0) | 2022.08.21 |
|---|---|
| 16398 행성 연결 (0) | 2022.08.20 |
| 1647 도시 분할 계획 (0) | 2022.08.09 |
| 1197 최소 스패닝 트리 (0) | 2022.08.08 |
| 9226 도깨비말 (0) | 2022.07.31 |