[코드포스 Practice4] E. Modular Equations
Last week, Hamed learned about a new type of equations in his math class called Modular Equations. Lets define i modulo j as the remainder of division of i by j and denote it by
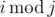
A Modular Equation, as Hamed's teacher described, is an equation of the form
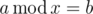
in which a and b are two non-negative integers and x is a variable. We call a positive integer x for which
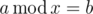
a solution of our equation.
Hamed didn't pay much attention to the class since he was watching a movie. He only managed to understand the definitions of these equations.
Now he wants to write his math exercises but since he has no idea how to do that, he asked you for help. He has told you all he knows about Modular Equations and asked you to write a program which given two numbers a and b determines how many answers the Modular Equation
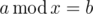
has.
Input
In the only line of the input two space-separated integers a and b (0 ≤ a, b ≤ 109) are given.
Output
If there is an infinite number of answers to our equation, print "infinity" (without the quotes). Otherwise print the number of solutions of the Modular Equation
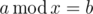

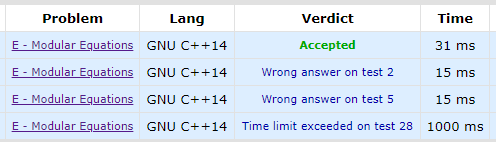
D번 풀고 나니 40분 남았길래 아 5솔브 갈 수 있겠다~!~! 싶었지만 여기서 전사..
문제 이해하기는 쉬웠는데 도저히 모르겠다ㅋㅋㅋ 처음에는 그냥 for문으로 셀까 싶었는데 입력이 10억이라 불가능했다. (O(n)일때 시간복잡도는 1-2억! 터무니없다)

규칙 찾는다고 보니 절반 이후로는 수가 한 번씩 나온다? 그래서 절반까지 count++를 하고 마지막에 +1만 해주면 되겠다 싶었다. 그런데 절반으로 나눠도 for문은 5억번 돈다ㅋㅋㅋ
다음으로 5를 보니 16에다 8이다. 그래서 아 여기 뭔가 있을 것 같은데 싶어서 그럼 처음 나머지가 5인 값의 배순가?? 했지만 틀렸다. 지금 생각해보니 1이면 어쩔뻔했어
그러다 끝났다.. 미해결이고 감도 못 잡음...
오.. 일단 a%x = a 인 경우는 무한히 많아서 제외 10 % 1000 = 10, 10 % 20 = 10 이므로 x > a이기만 하면 다 a가 나온다. 다음으로 a % x = b 인데 b가 a보다 큰 경우는 없다. 그래서 이때는 0을 출력한다. 그래서 a > b인 경우만 확인하면 된다.
a mod x = b 는 (a-b) mod x = 0; 이어야 한다. 즉, x는 a-b의 약수이다! 그리고 x > b여야한다.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <functional>
using namespace std;
using i64 = long long;
int main() {
int a, b;
scanf("%d %d", &a, &b);
if(a == b){
printf("infinity");
return 0;
}
if(b > a){
printf("0");
return 0;
}
int n = 0;
for(int i = b+1; i <= (a-b); i++){
if((a-b)%i == 0)
n++;
}
printf("%d", n);
return 0;
}
앗 이번에는 28까지 갔는데 시간초과가 떴다. 어떻게 하면 O(sqrt(a)) 만큼 돌지???
int main()
{
int a, b;
scanf("%d %d", &a, &b);
if (b == a)
{
printf("infinity\n");
return 0;
}
a -= b;
int ans = 0;
for (int i = 1; i * i <= a; i++)
{
if (a % i != 0)
continue;
if (i > b)
ans++;
if (a / i != i && a / i > b)
ans++;
}
printf("%d\n", ans);
return 0;
}아하.. 이게 for (int i = 1; i * i <= a; i++) 이렇게 돌아야 루트 n번 돌겠구나.. 신기하다. 그리고 내 코드는 x는 a-b의 약수이고 x > b여야 해서 반복문으로 b ~ (a-b)까지 돌았는데 이렇게 하면 O(n)만큼 돌겠다.
궁금해서 찾아보니 왜 sqrt만큼 도는지 증명해놓은게 많다.
이거 참고해서 공부했음. 근데 왜 이렇게 되는지 내가 설명하긴 어렵다. 약수 보면 두개가 있으니깐.. 두개 두개로 묶을 수 있는데.. 그 중간점이 sqrt(n).. 그 반까지만 확인하면.. 된다.. 아래 그림을 보면 알 수 있을 것입니다..

루트 i까지 도는데 만약 i가 나눠지면 i는 약수라는 뜻이다. 그래서 그 때 i랑 (a-b)/i가 b보다 큰지 확인한다. 처음에는 둘 다 if로 짰는데 그러면 제곱일 경우 한번 더 더하고, 두번째는 if랑 else if로 짰는데 그러면 i>b인 경우는 확인을 안 하고 지나치는 문제가 있었다. 그래서 코드 좀 더럽지만 제곱인 경우 / 아닌 경우 나눠서 생각했다.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <cmath>
using namespace std;
using i64 = long long;
int main() {
int a, b;
scanf("%d %d", &a, &b);
if(a == b){
printf("infinity");
return 0;
}
if(b > a){
printf("0");
return 0;
}
int n = 0;
for(int i = 1; i*i <= (a-b); i++){
if((a-b)%i == 0){
if(i == (a-b)/i){
if(i > b)
n++;
}
else{
if((a-b)/i > b)
n++;
if(i > b)
n++;
}
}
}
printf("%d", n);
return 0;
}와~~~ 햄복해
해결했음
int main()
{
int a, b;
scanf("%d %d", &a, &b);
if (b == a)
{
printf("infinity\n");
return 0;
}
a -= b;
int ans = 0;
for (int i = 1; i * i <= a; i++)
{
if (a % i != 0)
continue;
if (i > b)
ans++;
if (a / i != i && a / i > b)
ans++;
}
printf("%d\n", ans);
return 0;
}다시 돌아와서 북님 코드
아 그러고 보니 b > a인 경우는 애초에 반복 조건을 만족하지 않겠구나. 굳이 나눌 필요가 없었겠다.
옹.. 먼저 0으로 안 나눠지면 패스하고 나눠지면 i > b인지 확인한다. 다음으로 a/i>b인지 확인하는데 a/i != i여야 한다. (제곱수가 아니어야한다) 아 이렇게 제곱수일때랑 아닌 때 코드를 합쳐 적을 수 있겠구나.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <cmath>
using namespace std;
using i64 = long long;
int main() {
int a, b;
scanf("%d %d", &a, &b);
if(a == b){
printf("infinity");
return 0;
}
int n = 0;
for(int i = 1; i*i <= (a-b); i++){
if((a-b)%i == 0){
if((a-b)/i > b && (a-b)/i != i)
n++;
if(i > b)
n++;
}
}
printf("%d", n);
return 0;
}그래서 수정했다. 코포 4도 끝~~ 이제 백준이나 풀러 가야지