마주하고 말았다. 세그먼트 트리
세그먼트 트리
구간을 반복해서 2등분 한 뒤 각각의 잘린 구간이 자신의 구간인 대푯값을 저장하고 관리하게 만드는 자료구조
query: O(logN)
update: O(logN)
query는 정확히는 O(2logN)
레벨당 2개의 노드만 건드리게 된다.
구현
full binary tree 형태를 가지기 때문에 힙처럼 구간의 모든 값을 배열에 저장할 수 있다.
어떤 노드의 번호가 idx면 왼쪽 자식은 2 * idx, 오른쪽 자식은 2 * idx + 1
배열의 크기는 4 * n 이상으로 설정해야 한다
int query(int l, int r, int node, int nodeL, int nodeR) {
if (l <= nodeL && nodeR <= r)
return data[node];
int mid = (nodeL + nodeR) / 2;
if (mid < l)
return query(l, r, node * 2 + 1, mid + 1, nodeR);
if (mid + 1 > r)
return query(l, r, node * 2, nodeL, mid);
return query(l, r, node * 2, nodeL, mid) + query(l, r, node * 2 + 1, mid + 1, nodeR);
}쿼리 범위: l, r
노드가 나타내는 범위: nodeL, nodeR
노드가 나타내는 범위가 쿼리 범위 l ~r에 포함된다면 해당 노드의 값을 그대로 리턴해준다
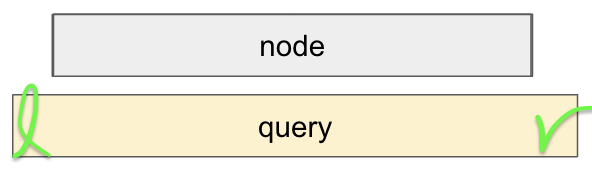
쿼리할 구간이 좌측 절반, 또는 우측 절반만 겹칠 경우 해당 절반만 쿼리해준다

나머지 경우는 왼쪽 오른쪽 자신 전부를 다 봐야 하는 경우라 양쪽 쿼리한 결과를 더해준다
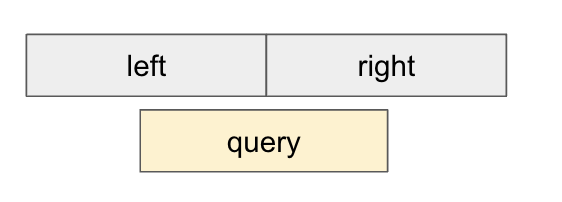
int update(int idx, int val, int node, int nodeL, int nodeR) {
if (idx < nodeL || idx > nodeR)
return v[node];
if (nodeL == nodeR)
return v[node] = val;
int mid = (nodeL + nodeR) / 2;
return v[node] = update(idx, val, node * 2, nodeL, mid) +
update(idx, val, node * 2 + 1, mid + 1, nodeR);
}- 업데이트 할 인덱스와 상관 없는 경우 갱신할게 없으므로 원래 값 리턴후 종료
- 리프노드에 도달했을 경우 해당 리프노드의 값을 새 값으로 갱신
- 그게 아니면 양쪽 자식 똑같이 갱신해주고 바뀐 값으로 내 노드도 갱신
int init(vector<int> &arr, int node, int start, int end) {
int mid = (start + end) / 2;
if (start == end)
return v[node] = arr[start];
return v[node] = init(arr, node * 2, start, mid) + init(arr, node * 2 + 1, mid + 1, end);
}특정한 초기값으로 설정해줄 때 쓸 수 있다.
'공부합시다' 카테고리의 다른 글
| 유클리드 호제법 (0) | 2024.11.16 |
|---|---|
| 외판원순회 (0) | 2023.07.22 |
| 플로이드 와샬 알고리즘 (0) | 2022.12.17 |
| 순열 (1) | 2022.10.01 |
| offset 대신 포인터로 사용하기 (0) | 2022.08.31 |

