Little Joty has got a task to do. She has a line of n tiles indexed from 1 to n. She has to paint them in a strange pattern.
An unpainted tile should be painted Red if it's index is divisible by a and an unpainted tile should be painted Blue if it's index is divisible by b. So the tile with the number divisible by a and b can be either painted Red or Blue.
After her painting is done, she will get p chocolates for each tile that is painted Red and q chocolates for each tile that is painted Blue.
Note that she can paint tiles in any order she wants.
Given the required information, find the maximum number of chocolates Joty can get.
Input
The only line contains five integers n, a, b, p and q (1 ≤ n, a, b, p, q ≤ 109).
Output
Print the only integer s — the maximum number of chocolates Joty can get.
Note that the answer can be too large, so you should use 64-bit integer type to store it. In C++ you can use the long long integer type and in Java you can use long integer type.

전에 풀었던 거 보니 왜 저렇게 풀었지...? 싶어서 다시 풀었다.
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <functional>
using namespace std;
using i64 = long long;
int main() {
i64 n, a, b, p, q;
scanf("%lld %lld %lld %lld %lld", &n, &a, &b, &p, &q);
i64 choco = 0;
for(i64 i = 1; i <= n ; i++){
if(i%a == 0 && i%b == 0){
if(p>q)
choco += p;
else
choco += q;
}
else if(i%a == 0)
choco += p;
else if(i%b == 0)
choco += q;
}
printf("%lld", choco);
return 0;
}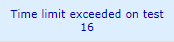
그렇게 짰던 이유가 있었다. 시간초과했음; 머쓱

다시 들고오는 시간복잡도 사진
이렇게 짜면 시간복잡도가 O(N)이므로 N이 1억까지 가능하다. 그런데 나는 10억을 넣어서 문제였음.
다시 생각해보러 가야지

전처럼 개수로 다뤄야겠다 생각해서 로직을 짜봤다. 간단하다! 공배수만 구할 수 있다면
그래서 공배수 어떻게 구하지 고민하다가 전에 유클리드로 재귀함수 써서 구한 거 생각나서 블로그를 뒤져봤다.
기록은 항상 도움이 된다

그러하다.. GCD(a, b) = GCD(b, a%b) ......
나머지가 0이 될 때 b가 최대공약수..
최소공배수는 (a * b) / 최대공약수
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <functional>
using namespace std;
using i64 = long long;
i64 GCD(i64 a, i64 b){
if(b == 0)
return a;
return GCD(b, a%b);
}
i64 LCM(i64 a, i64 b){
return (a*b)/GCD(a, b);
}
int main() {
i64 n, a, b, p, q;
scanf("%lld %lld %lld %lld %lld", &n, &a, &b, &p, &q);
i64 choco = 0;
i64 lcm = LCM(a, b);
if(p > q)
choco += n/lcm*p;
else
choco += n/lcm*q;
choco += (n/a-n/lcm)*p;
choco += (n/b-n/lcm)*q;
printf("%lld", choco);
return 0;
}
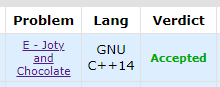
dhk~~~~
멤모))
return (a*b)/GCD(a, b);
여기서 a*b를 먼저 곱하고 GCD를 나누는 게 아니라 a / GCD * b 로 계산하는 게 더 좋다.
a*b하다가 터질 수 있음,,
'코드포스' 카테고리의 다른 글
| [코드포스 Practice6] A. Police Recruits (0) | 2019.12.03 |
|---|---|
| [코드포스 Practice6] 후기 (0) | 2019.12.03 |
| [코드포스 Practice5] D. K-Dominant Character (0) | 2019.11.27 |
| [코드포스 Practice5] C. Mind the Gap (0) | 2019.11.27 |
| [코드포스 Practice5] B. Oath of the Night's Watch (0) | 2019.11.27 |



